トップページ>研究室紹介
研究内容について
微小化により付加価値を増大させる近未来の工学
有限要素法(FEM)に代表されるCAE(Computer Aided Engineering)の実施には,以前は高性能計算機が必須であったが,現在ではPC上でのパッケージソフトとして多くの製造業の企業で利用されている.これは,現在のPCワークステーション(数十万円オーダー)の性能が20年前のスーパーコンピュータ(数億円オーダー)のそれを凌駕するという,計算機の指数関数的性能向上に負うところが大きい.機械産業は,20世紀に重厚長大の極値に達したが,現在では小型化・微小化することで高付加価値を達成する方向にシフトしており,特にMEMS(日本語ではマイクロマシン)技術の進展が著しい.機械における微小化は半導体技術を範としている.その代表であるコンピュータ用のCPUは現行7 nm(1,000,000 nm = 1 mm)プロセスで製造されており,Siチップ上の配線幅は原子70個程度である.すなわち,最先端分野においては,材料は微視的に原子の集合体として扱う必要がある.自然現象の根本は原子の運動状態の変化
このような現状を踏まえ,当研究室では将来のCAEの一翼を担うべく,原子・分子レベルでのシミュレーションである分子動力学法の機械材料,流体,トライボロジーなどの各分野への適用に関する研究を行っている.分子動力学法により,作動中の機械を構成する固体・液体・気体の微視的な状態やそれらの高速な変化が統合的に解析できる.最近の機械では高性能化を意図して内部要素の微小化が進んでいるので.実験だけでは解明できない問題が増えている.当研究室での研究はその様な問題に対する解答を与えるものである.分子動力学法とは
FEM等では物体・流体を連続体として扱うが,それらを離散化した原子・分子の集合体の動力学として扱うのが分子動力学法(MD)である.分子動力学法では,原子(分子は原子が相互に拘束されたもの)間に作用する力は原子間ポテンシャル関数の位置微分として計算され,各原子の運動方程式は質点系の多体問題として時間で数値積分される.連続体としての挙動は,微視的にはそれを構成する個々の原子・分子の運動状態(位置と速度)とポテンシャルエネルギーの時間変化に対応している.原子・分子の運動状態やポテンシャルエネルギーについて,統計力学を用いて解析することにより,連続体レベルの巨視的な状態に加えて,実験では容易には知ることができない微視的な状態も評価できる.例えば,物体の温度はそれを構成する原子の運動エネルギーの平均から計算される.研究の焦点
当研究室では,工学上の種々の現象に対する分子動力学法によるシミュレーションを,約20台のPCワークステーションで実施している.大規模な場合では,数百万原子からなるモデルに対し数千万回の数値積分を行っている.分子動力学法の基本原理自体は物理学の分野で数十年の歴史がある.しかしながら,工学上の種々の実際の問題に適用する場合には,各現象を適切にモデル化することや,数値積分から得られる各原子の座標と速度の時系列データから工学的に有益な情報を得る解析手法については未解決な点が多く,研究の焦点となっている.以下,直感的に理解しやすいCGによる解析結果に絞って,研究例を紹介する.
研究例
研究例1:金属材料への飛翔体の高速衝突による破壊
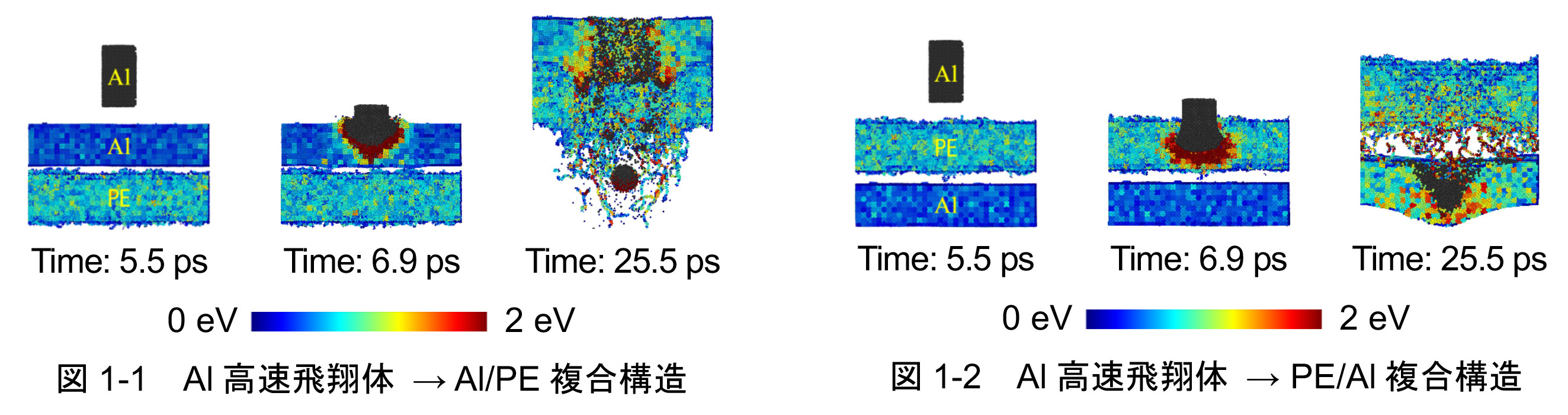
近年,宇宙空間上のスペースデブリの衝突(相対衝突速度10 km/sオーダー)による人工衛星の損傷が問題となっている.この現象では,非常に短時間で運動エネルギーが熱エネルギーと材料の変形・破壊に転換されるので,損傷の過程を材料組織レベル・原子レベルで実験によりリアルタイムで観察・測定することは困難である.分子動力学法により,円柱形状のAl金属飛翔体とAl/ポリエチレン(PE)からなる平板形状の複合構造との相対速度5 km/sでの衝突を,シミュレーションした結果の一例を示す.まず,モデルを234,744個のvoxel(一辺5.979 オングストロームの立方体積要素)に空間分割し,voxel毎の原子の運動エネルギーの平均値を局所量として計算する.次に,CGソフトウェアを使用して,局所量の断面のカラーマップのスナップショットとして可視化したものが下に示す2枚の図である.図1-1において,Al飛翔体が1層目のAl固体壁を侵徹する時,Al飛翔体の直下の領域で局所熱エネルギーが著しく上昇する(中央).局所熱エネルギーの最高値は71.2 eVである.さらに,その領域ではAl飛翔体とAl固体壁が融合した球形状の高密度Al原子群が形成される.その後,原子群は複合構造を貫通する(右).図1-2において,Al飛翔体が1層目のPE固体壁を侵徹する時,Al飛翔体は衝突面積が拡げられるように変形する(中央).Al飛翔体の重心並進運動エネルギーはPE固体壁内へと広範囲に散逸され,Al高密度領域は形成されず,複合構造の貫通が生じない(右).図1-1において,Al飛翔体が複合構造を貫通する原因は,Al飛翔体が固体壁を変形させ,局所密度が上昇し,その領域内の空間エネルギー密度が高くなるため,飛翔体衝突によって局所熱エネルギーが著しく上昇し,実質的に,固体壁を貫通するのに十分な飛翔体の重心並進運動エネルギーが維持されることにあると考えられる.
研究例2:ナノオーダーサイズの流れ場の解析
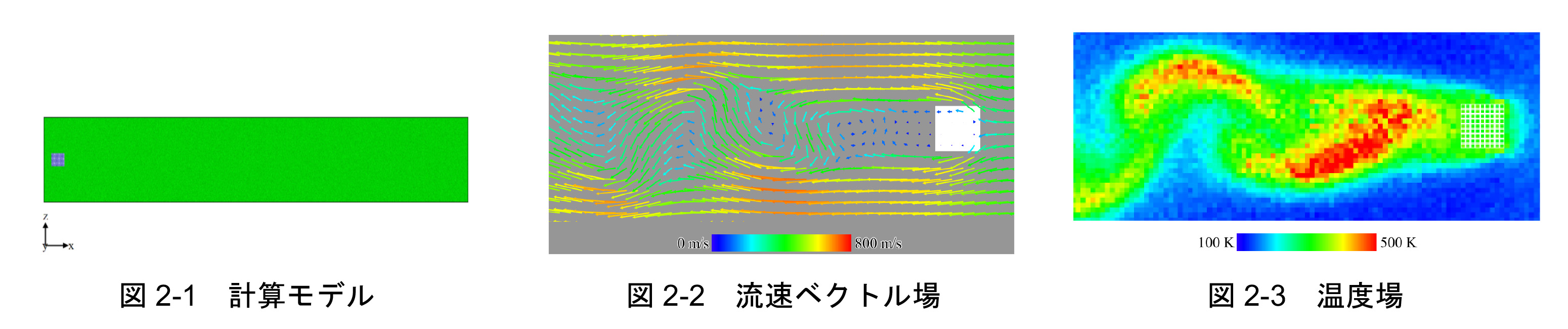
近年MEMS(マイクロマシン)の利用が拡大しており,超微小流路における流体の挙動をあらかじめ予測して,MEMSの設計を行う必要性が生じている.しかしながら,代表寸法がナノメートルサイズの流れにおいては,流体を構成する分子や原子の質点としての効果が無視できないので,連続体の力学として記述される流体力学の諸式のみでは不十分である.流れを薄い平板形状のモデルとして扱う擬3次元分子動力学法(MD)により,流体中を準定常的に並進運動するナノサイズの物体まわりの液体の流れをシミュレーションし,ナノサイズの流れの挙動を原子レベルで解析・可視化した結果の一例を示す.本モデルでは,図2-1の様に2,863,190個の流体分子(緑)中を四角柱(青)が左から右に運動する.Re30の場合の四角柱まわりの流速ベクトル場(図2-2)と温度場(図2-3)を示す.流速ベクトル場にみられる様にカルマン渦が生じている.温度場において,四角柱後方の流体が高温となっているのは,固体後方では流体の変形量が大きく,エネルギーの勾配が大きいためと考えられる.このような局所的な高温領域では流体の粘性率が局所的に減少し,カルマン渦が生じたと考えられる.また,同図からは、固体後方の高温流体が,カルマン渦によって後方へ運ばれる様子が確認できる.これにより,四角柱後方の流体の温度が減少すると,カルマン渦の生成は少なくなる.この様にナノスケールにおいても流体の相似則が成り立つことが示された.
研究例3:潤滑中の潤滑油の分子の構造とダイナミクス
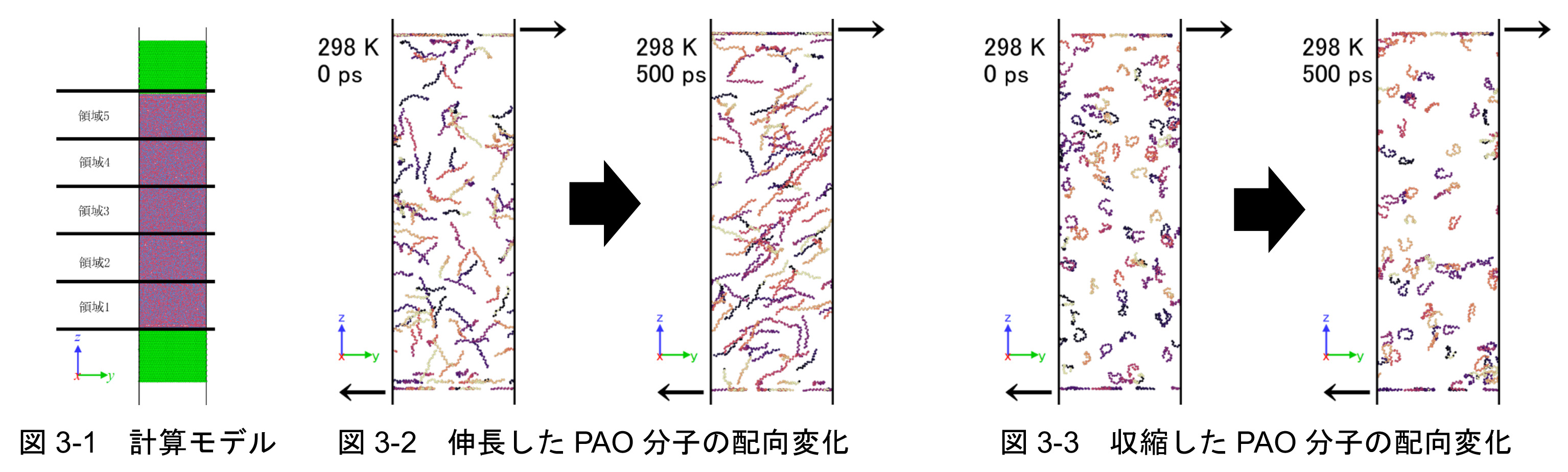
潤滑油を介した潤滑は機械において必要不可欠な要素であるが,現状では,動的な潤滑のミクロな状態をin situで実験的に観察することは困難であり,潤滑の理論的な定量予測を困難にしている.油膜の厚さが潤滑油の分子長オーダーとなった場合の準定常状態の潤滑を,分子動力学法によりシミュレーションした結果の一例を示す.シミュレーションには,図3-1に示す完全に平滑な2枚のNi固体平板に添加物の付与されていない純粋なC20H40のポリアルファオレフィン(PAO)2,304分子からなる油膜としての流体が挟まれたモデルを使用する.2枚のNi固体平板をそれぞれ水平逆方向に等速直線運動させることで,潤滑をシミュレーションする.油膜中のPAO分子は,その内部自由度に基づき様々な形状を示すが,伸長したもの(全長20.5 Å以上)および収縮したもの(全長7 Å以下)のみを選択して可視化した結果を図3-2と図3-3に示す.油膜にせん断が付加される前(0 ps)と付加された後(500 ps)を比較すると,せん断により,伸長したPAO分子の数はかなり増大するとともにせん断方向に分子の配向を生じる.一方,収縮したPAOの数は減少するがその配向はせん断の影響を受けていない.
研究例4:HDDのプラッタとヘッドを想定したシミュレーション
分子動力学法により,ハードディスク(HDD)の磁気ヘッドとプラッタ(ディスク)を想定したモデル(モデル化のために周期境界条件を適用してある)の計算結果を可視化した一例を下に示す.橙色球で示す平行平板が磁気ヘッドとプラッタに対応し,互いに逆方向に直線運動をしている.両者の間隔は最新のHDDに対応する10 nmである.一部の気体分子の軌跡を緑色線で,その最終位置を紫色球で示してある.固体表面と複雑な衝突をする気体分子,固体表面に物理吸着して熱振動する気体分子,気体分子同士の衝突等が生じている様子がわかる.また,このような分子流と固体との間の摩擦力も解析評価している.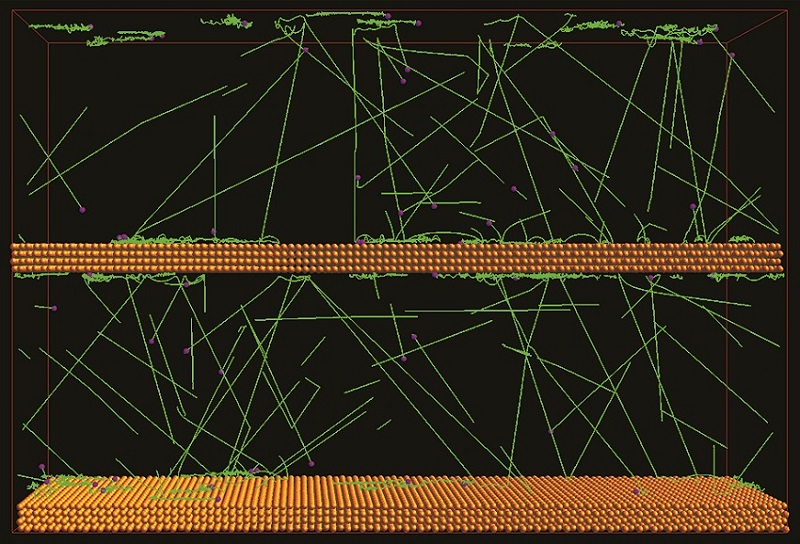 図 4 HDDのプラッタとヘッド(オレンジ)および気体分子の軌跡(緑)
図 4 HDDのプラッタとヘッド(オレンジ)および気体分子の軌跡(緑)